В рубрике "Математические неожиданности " неоднократно приводились числовые примеры, которые читаются одинаково как слева направо, так и справа налево - числовые палиндромы. Они возникают при возведении в квадрат или при перемножении некоторых пар чисел, например: 12^.42 = 21^.24; 13² = 169, 961 = 31² (см. "Наука и жизнь" № 11, 1968 г., № 10, 1971 г.). Продолжив тему этой палиндромной математики, которую можно было бы назвать палиндроматикой, попытаемся теперь решить другую задачу: найти все пары таких двузначных чисел N₁ = 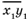и N₂ = 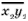(x - первая цифра, y - вторая), чтобы результат их сложения не менялся при прочтении суммы справа налево:

х₁у₁ + х₂у₂ = = + (*).

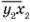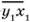Например:

42 + 35 = 53 + +24.

Поскольку двузначные числа N₁ = 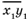и N₂ = 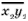можно записать соответственно в виде N₁ = 10х₁ + у₁ и N₂ = 10x₂ + y₂ , то равенство (*) приводится к виду (10х₁ + +у₁) + (10х₂ + у₂) = (10у₂ + х₂) + +(10у₁ + х₁), или 9(х₁ - у₁) = 9(у₂ - х₂). Отсюда окончательно х₁ + х₂ = у₁ + у₂, то есть сумма первых цифр у всех таких пар чисел равна сумме их вторых цифр. Теперь можно без труда строить подобные примеры:

76 + +34 = 43 + 67,

25 + 63 = 36 + +52 и т. д.

Аналогичным образом такая же задача легко решается для остальных арифметических действий. В случае разности (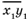- 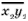= 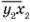- 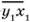) получается, например: 41- 32 = 23 - 14, 46 - 28 = 82 - 64, ... - суммы цифр у таких чисел равны (х₁ + у₁ = х₂+ + у₂).

Для умножения имеем: 63^.48 = 84^.36, 82^.14 = 41^.28, ... - произведение первых цифр у чисел N₁ и N₂ равно произведению их вторых цифр (х₁^. х₂ = у₁^.у ₂).

Наконец, для деления получаем:

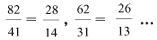
- произведение первой цифры числа N₁ на вторую цифру числа N₂ равно произведению двух других их цифр: х₁^.у ₂ = х₂^.у ₁ (вы заметили связь между примерами на деление и умножение?).

Попробуйте теперь решить подобную задачу для суммы (разности, произведения, отношения) двух трехзначных чисел, трехзначного и двузначного и других чисел. Быть может, вам придут в голову другие идеи ...

№5, 1998