Четыре рыцаря. Таб. 1.

Четыре рыцаря. Таб. 2.

Существует определенная закономерность, в соответствии с которой ряд широкоупотребительных кратких форм прилагательных в мужском и среднем роде имеет такое же ударение, как полная форма (на основе), а в женском роде ударение перемещается на окончание:

блЕдный - блЕден - бледнА - блЕдно - блЕдны

блИзкий - блИзок - близкА - блИзко - блИзки

врЕдный - врЕден - вреднА - врЕдно - врЕдны

глУпый - глуп - глупА - глУпо - глУпы

голОдный - гОлоден - голоднА - гОлодно - гОлодны

гОрький - гОрек - горькА - гОрько - гОрьки

грУбый - груб - грубА - грУбо - грУбы

густОй - густ - густА - гУсто - гУсты

дешёвый - дёшев - дешевА - дёшево - дёшевы

дрУжный - дрУжен - дружнА - дрУжно - дрУжны

жАлкий - жАлок - жалкА - жАлко - жАлки

крЕпкий - крЕпок - крепкА - крЕпко - крЕпки

пустОй - пуст - пустА - пУсто - пУсты

рЕдкий - рЕдок - редкА - рЕдко - рЕдки

Некоторые из этих прилагательных имеют во множественном числе допустимую параллельную форму с ударением на окончании:

бледнЫ, близкИ, вреднЫ, густЫ, дружнЫ.

Что касается кратких форм страдательных причастий, то здесь надо запомнить следующее правило: если в полной форме ударение падает на суффикс (-онн/-енн), то таким же оказывается ударение в краткой форме мужского рода. В женском и среднем роде и во множественном числе ударение перемещается на окончание:

введённый - введён - введенА - введенО - введенЫ

ввезённый - ввезён - ввезенА - ввезенО - ввезенЫ

Многие краткие причастия имеют ударение на первом слоге основы во всех формах, кроме единственного числа женского рода, где оно переходит на окончание:

зАнятый - зАнят - занятА - зАнято - зАняты

нАчатый - нАчат - начатА - нАчато - нАчаты

прИнятый - прИнят - принятА - прИнято - прИняты

взЯтый - взЯт - взятА - взЯто - взЯты

***

Вот как правильно произносятся эти слова:

ждАло (дитя ждАло подарка), эспАндер, чайнвОрд, табУ, термобигудИ, каталОг, тАндемный, нефтепровОд, облегчИть, отшпИлить, никелировАние, отрЯхнутый, полУнОчный.

Н. РЕВЕНСКАЯ.

УМНЫЕ ПАЛЬЦЫ (№ 9, 1998 г.)

- Ну, ладно, - согласился Борг, слегка покраснев. - Не будем об этом. Главное в другом. Вы заметили, что после "прочтения" пальцами маг всегда разворачивал записку и прочитывал ее глазами?

- Конечно, чтобы убедиться, что все правильно.

- В этом-то и состоит разгадка! А если добавить, что блондинка, как я думаю, работает заодно с магом, то все становится ясно.

- Мне пока ничего не ясно, - проворчал Глум, инстинктивно дотронувшись до кармана с бумажником. - При чем тут то, что он читал записки и глазами? Ведь это было после чтения пальцами.

- В том-то и дело, что нет. Ощупывая первую записку пальцами, он сделал вид, что прочитал ее, а на самом деле произнес заранее подготовленную фразу: "Я не верю в эту чепуху!". Соучастница мага, та самая блондинка, "призналась", что она написала эту фразу. Тогда маг, якобы желая лично убедиться в правильности "прочтения" пальцами, достал записку, якобы написанную блондинкой. А на самом деле это была ваша записка! Он про себя прочитал ее и запомнил. Затем, нащупав в мешке следующую записку, произнес вслух вашу фразу про блондинок и снова, как бы желая убедиться в правильности своего "прочтения", развернул и прочитал ее про себя. Ну и так далее. Последней он достал особо помеченную (например, согнутую пополам) записку блондинки.

- Да, хитро придумано, - согласился Глум. - Но я поверю в эту версию, только если смогу убедиться, что красотка играет в одной команде с фиктивным магом.

- А вы посмотрите туда, - с усмешкой посоветовал инспектор, указывая на полуприкрытый вход в шатер.

В глубине помещения Глум отчетливо увидел мага, обсуждающего что-то с блондинкой. Даже с такого расстояния сержанту было понятно: они хорошо знакомы.

- Эх, - сокрушенно вздохнул Глум, доставая из бумажника проигранные деньги, - никогда больше не буду верить ни чудесам, ни женщинам.

НА ШАХМАТНОМ ТУРНИРЕ (№ 6, 1998 г.)

Количество партий, сыгранных в ходе однокругового турнира, подсчитывается по формуле (ее легко вывести самим)

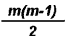
где m - количество участников.

Пусть m - количество шахматистов, играющих в секции Б. Тогда

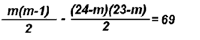
Решив уравнение, получим m = 15.

Следовательно, в секции А 24-15=9 шахматистов.

Слонов играл восемь партий. Значит, пять партий из них он свел вничью: 5 ¹/₂ = 3+2^.1/₂.

ЧЕТЫРЕ РЫЦАРЯ (№ 7 , 1998 г.)

Чтобы фиксировать ход логических рассуждений, составим таблицу и внесем в нее данные из условия задачи.

Выпишем ограничения, наложенные условием задачи. Серебристый щит, серебристое забрало и оранжевый султан явно не принадлежат сэру Брюсу. Кроме того, есть пары деталей снаряжения, каждая из которых принадлежит одному хозяину:

пурпурный щит и оранжевое забрало;

оранжевый щит и серебристый султан;

сиреневый щит и серебристый флажок;

сиреневое забрало и пурпурный флажок;

сиреневый султан и оранжевый флажок.

Последняя из пар принадлежит брату сэра Каспара. Из анализа пар следует вывод: у сэра Каспара щит не пурпурный, султан не сиреневый, а флажок не оранжевый и не пурпурный. Следовательно, флажок у него серебристый, а щит - сиреневый (см. пары). Запишем добытые данные в таблицу 1.

Теперь видно, что оранжевый флажок может быть либо у сэра Альбуса, либо у сэра Брюса. Исследуем второй вариант. В этом случае у сэра Альбуса флажок пурпурный и, значит, сиреневое забрало (см. пары), а у сэра Брюса сиреневый султан. Уже известно, что серебристое забрало не может принадлежать сэру Брюсу. Следовательно, у него забрало оранжевое (других вариантов не осталось), а щит - пурпурный (см. пары). Попутно заметим, что серебристое забрало осталось на долю сэра Даниэля. Но у него не может быть серебристый щит (он и забрало того же цвета принадлежат разным хозяевам). Следовательно, щит у сэра Даниэля оранжевый, соответственно - серебристый султан. А серебристый щит может быть только у сэра Альбуса.

Теперь ясно, кто на какой лошади сидит. У сэра Альбуса - Евангелина, у сэра Даниэля - Геркулес, а у сэра Каспара, следователь но, Фурия. Стало быть, у сэра Каспара султан оранжевый (см. условие). В конце концов выясняется, что пурпурный султан, обладатель которого заинтересовал королеву, украшает шлем сэра Альбуса. Задача решена.

Добавим, что исследование первого варианта (оранжевый флажок у сэра Альбуса) выявит противоречия с условием задачи.

В окончательном виде таблица выглядит так (см. таблицу 2).

№9, 1998