РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ И СТАТИКИ
Кандидат физико-математических наук В. ПОГОЖЕВ.
Продолжаем публиковать разбор конкурсных задач по физике, которые в последние годы предлагались поступающим на физический факультет МГУ.
Задача 3 (1998 г.). Космический корабль движется по круговой орбите вокруг Земли так, что все время находится на прямой, соединяющей Землю и Луну, на таком расстоянии, что действие их гравитационных сил на корабль уравновешено. Найти вес космонавта в корабле, если масса космонавта равна m, отношение масс Земли и Луны равно k, радиус орбиты Луны в n раз больше радиуса Земли, а ускорение свободного падения у поверхности Земли равно g.
Решение. Будем решать задачу, используя геоцентрическую систему отсчета, считая ее инерциальной, то есть не станем учитывать орбитального движения Земли. Одновременно пренебрежем влиянием всех остальных небесных тел на движение Луны и космического корабля. По условию задачи орбиту Луны следует считать круговой. Поэтому на основании второго закона Кеплера можно утверждать, что Луна по своей орбите движется равномерно. Следовательно, согласно законам кинематики, ее ускорение направлено к центру Земли и равно аn = ω Rл, где ω — угловая скорость, а Rл — радиус орбиты Луны. При сделанных предположениях можно утверждать, что ускорение Луны обусловлено действием на нее только гравитационных сил со стороны Земли (массой космического корабля можно пренебречь). Тогда, согласно закону всемирного тяготения и второму закону Ньютона, пренебрегая размерами Луны, получим
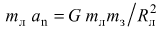 ,
,
где G — гравитационная постоянная, а mл и mз — массы Луны и Земли соответственно.
Учитывая, что ускорение свободного падения на полюсе вблизи поверхности Земли
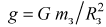 ,
,
из написанных соотношений следует, что угловая скорость движения Луны, а следовательно, и космического корабля (так как он все время остается на прямой, соединяющей Землю и Луну) равна
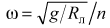 .
.
Здесь учтено, что по условию задачи
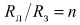 .
.
По условию задачи космический корабль находится на таком расстоянии r от Земли, что гравитационные силы, действующие на него со стороны Земли и Луны, уравновешивают друг друга. Это, согласно закону всемирного тяготения, возможно только в том случае, если с учетом ранее сделанных предположений выполняется соотношение
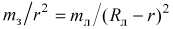 .
.
Поскольку по условию задачи
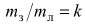 ,
,
то радиус орбиты корабля
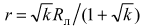 .
.
Следовательно, центростремительное ускорение корабля определяется соотношением
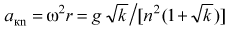 .
.
Поскольку действия Земли и Луны на корабль скомпенсированы, а действием всех других небесных тел мы пренебрегаем и считаем геоцентрическую систему отсчета инерциальной, вычисленное ускорение может быть обеспечено только за счет работы двигателей самого корабля. Пренебрегая размерами корабля по сравнению с радиусом его орбиты, следует считать, что такое же ускорение относительно инерциальной системы отсчета имеет и космонавт. Поэтому на основании второго закона Ньютона получаем, что на космонавта корабль должен действовать с силой F=maкn . Следовательно, согласно третьему закону Ньютона, вес космонавта в системе отсчета, связанной с кораблем, равен
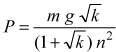 .
.
Задача 4 (2000 г.). На горизонтальном диске на расстоянии R от его оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время τ после начала раскручивания шайба стала скользить по диску. Найти коэффициент трения шайбы о диск, если за время τ диск сделал n оборотов.
Решение. Поскольку диск первоначально покоился и его угловую скорость увеличивают с постоянным угловым ускорением ε, по аналогии с законами изменения проекции скорости и координаты точки при прямолинейном равнопеременном движении можно утверждать, что к моменту времени τ угловая скорость диска должна стать равной ω(τ)=ετ и диск должен повернуться на угол φ(τ) = ετ 2/2. За один оборот диск поворачивается на угол 2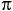 , по условию задачи он за время τ совершил n оборотов, поэтому из написанных выше выражений следует, что диск раскручивали с угловым ускорением ε=4
, по условию задачи он за время τ совершил n оборотов, поэтому из написанных выше выражений следует, что диск раскручивали с угловым ускорением ε=4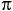 ν/τ.
ν/τ.
По определению, длина дуги окружности радиуса R, заключенная между радиусами, образующими угол φ, равна Rφ. Следовательно, тангенциальная составляющая ускорения точки диска, находящейся на расстоянии R от оси вращения, равна αφ=εR. Вспоминая, что нормальная составляющая ускорения точки, движущейся с угловой скоростью со по дуге с радиусом кривизны R, равна
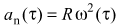 ,
,
можно утверждать, что ускорение шайбы к моменту времени τ относительно лабораторной системы отсчета, в которой ось диска неподвижна, должно стать равным
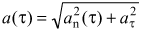 .
.
Считая, как обычно, указанную систему отсчета инерциальной и пренебрегая действием воздуха на шайбу, можно утверждать, что ускорение шайбы обусловлено действием на нее только тангенциальной составляющей силы реакции диска (плоскость диска по условию задачи горизонтальна). Поэтому, согласно второму закону Ньютона, максимальное значение тангенциальной составляющей силы реакции диска — силы сухого трения — должно быть равно
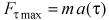 .
.
Учитывая, что при выполнении сделанных ранее предположений шайба прижимается к диску только за счет действия на нее силы тяжести, нормальная составляющая силы реакции диска должна быть равна N=mg, где g — ускорение свободного падения. Поэтому, вспоминая закон Кулона—Амона для сил сухого трения, можно утверждать, что μ= Fτmax /N. Подставив в это выражение ранее полученные соотношения, определим искомый коэффициент трения шайбы о диск
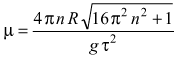 .
.
Задача 5 (1997 г.). Из тонкого резинового шнура массой m жесткостью k изготовили кольцо радиусом r. Каким стал бы радиус кольца, если бы оно вращалось равномерно с угловой скоростью ω вокруг своей оси?
Решение. Из кинематики известно, что ускорение движущейся по криволинейной траектории точки в общем случае можно представить в виде суммы двух компонент: нормальной аn, направленной по радиусу кривизны траектории, и тангенциальной аτ, направленной по касательной к траектории в сторону возрастания траекторной координаты и характеризующей быстроту изменения проекции скорости на это направление. Требуется определить радиус кольца при заданной угловой скорости вращения, то есть когда все точки кольца движутся равномерно, аτ равно нулю. В условии задачи не указано, какие тела действуют на кольцо и как расположена его ось. Выбрав из всех возможных случаев простейший, будем считать, что ось кольца неподвижна относительно инерциальной системы отсчета, и так как вращение кольца происходит с постоянной скоростью, действие окружающих тел на любую из точек кольца скомпенсировано. Кольцо сделано из тонкого шнура, все точки которого находятся на одинаковом расстоянии от его оси и их ускорение равно αn=ω2R, где R — искомый радиус кольца.
Это ускорение при сделанных предположениях могут обеспечить лишь силы натяжения, возникающие за счет упругой деформации шнура. На рис. 5 показаны участок вращающегося кольца, ограниченный радиусами R, образующими малый угол ∆α, и силы, действующие на него со стороны соседних участков. Поскольку эти силы направлены по касательным к оси кольца в соответствующих точках и тангенциальная составляющая ускорения точек кольца равна нулю, модули этих сил — сил натяжения — должны быть равны. Считая, что при заданной угловой скорости применим закон Гука, величина силы натяжения
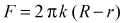 .
.
Силы натяжения, действующие на концы рассматриваемого участка, направлены перпендикулярно соответствующим радиусам, их результирующая равна 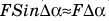 и направлена к оси вращения. Поэтому на основании второго закона Ньютона можно утверждать, что
и направлена к оси вращения. Поэтому на основании второго закона Ньютона можно утверждать, что
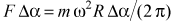 ,
,
так как рассматриваемый участок кольца можно в силу малости угла ∆α принять за материальную точку массой
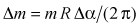 .
.
Из написанных уравнений следует, что при сделанных предположениях радиус кольца при заданной угловой скорости вращения должен быть равен
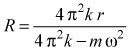 .
.
Из этого выражения видно, что при увеличении угловой скорости вращения до
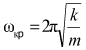
радиус кольца должен неограниченно возрастать, то есть кольцо разорвется. В действительности разрушение кольца произойдет при несколько меньшей угловой скорости ωп, когда силы натяжения кольца достигнут величины Fmax, при которой нарушается закон Гука. Таким образом, если угловая скорость вращения кольца
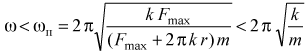 ,
,
то искомый радиус кольца равен
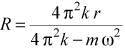 .
.
При попытке заставить кольцо вращаться с угловой скоростью ω>ωп кольцо должно разорваться.
Задача 6 (2000 г.). В узкую прямоугольную кювету налили воду и положили два гладких одинаковых цилиндра так, что их оси оказались горизонтальны и параллельны длинным стенкам кюветы. При этом цилиндры касались стенок кюветы только своими образующими, верхний цилиндр погрузился в воду наполовину, а нижний — касался ее поверхности своими верхними точками. Найти силы, действующие со стороны цилиндров на стенки кюветы, если объем каждого из них равен V=20 см3.
Решение. Будем решать задачу, полагая, что торцы цилиндров находятся на одинаковом расстоянии от параллельных им стенок кюветы, кювета с ее содержимым покоится относительно ЛСО и эту систему можно считать инерциальной. Верхний цилиндр погружен в воду наполовину, поэтому можно утверждать, что равнодействующая F1 сил гидростатического давления на верхний цилиндр должна быть равна -ρVg/2, где g~9,8 м/с2 — ускорение свободного падения, а ρ~1 г/см3 — плотность воды. Действующая же со стороны воды на полностью погруженный нижний цилиндр сила будет в два раза больше и равна F2=-ρVg. Из соображений симметрии ясно, что линии действия сил F1 и F2 должны пересекать середины осей цилиндров под прямым углом. Поскольку по условию задачи цилиндры гладкие, силы их взаимодействия должны лежать в плоскости, проходящей через оси цилиндров, и быть перпендикулярными этим осям. Перпендикулярными осям цилиндров, но направленными горизонтально будут и силы реакции со стороны стенок кюветы, так как эти стенки вертикальны. Вспомнив, что при равновесии сумма моментов действующих на твердое тело сил должна быть равна нулю, можно утверждать, что равнодействующие сил тяжести, действующих на цилиндры, должны лежать в вертикальных плоскостях, проходящих через их оси. Более того, опираясь на сказанное, можно доказать, что при заданном расположении цилиндров и выполнении сделанных предположений равнодействующие всех рассмотренных сил должны лежать в вертикальной плоскости, проходящей через середины этих цилиндров.
На рис. 6 показаны сечение кюветы вертикальной плоскостью, равнодействующие сил реакции стенок Fcl и Fc2, сил гидростатического давления F1 и F2, сил взаимодействия цилиндров N1 и N2 и сил тяжести. Буквами D и С обозначены точки приложения сил F1 и F2, а буквой m — масса цилиндра. Поскольку цилиндры находятся в равновесии, сумма всех сил, действующих на каждый из них, должна быть равна нулю и, следовательно, должны выполняться соотношения:
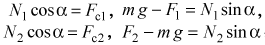 ,
,
причем, согласно третьему закону Ньютона, N1=N2.
Решая полученную систему уравнений с учетом того, что F2 = 2F1 = ρgV, силы взаимодействия двух тел равны по величине и треугольник ABC является прямоугольным, а потому sin α = ВС/AC = 0,5, определим искомые силы действия цилиндров на стенки кюветы:
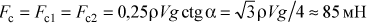 .
.
Задача 7 (2000 г.). Горизонтальная штанга длиной r, на конце которой закреплен груз массой m, вращается на подшипнике с угловой скоростью ω вокруг вертикальной стойки штатива высотой h (рис. 7). При какой угловой скорости основание штатива — тонкий диск массой М и радиусом R (R >r — перестанет касаться всей плоскостью горизонтальной поверхности стола? Массой штанги и стойки пренебречь. Считать, что диск не скользит по столу, а размеры груза существенно меньше r.
Решение. Все тела, указанные в условии, будем считать твердыми. Поскольку вращение груза по условию задачи происходит с неизменной угловой скоростью ω, то действием сил сопротивления движению штанги и груза следует пренебречь. Кроме того, как обычно, лабораторную систему отсчета, относительно которой штатив при достаточно малой угловой скорости вращения покоится, будем считать инерциальной. Тогда на основании второго закона Ньютона можно утверждать, что со стороны штанги на груз действует сила, горизонтальная составляющая которой обеспечивает грузу центростремительное ускорение —ω2r, а вертикальная составляющая уравновешивает действие на груз силы тяжести mg, где g — ускорение свободного падения.
Основываясь на сказанном и на третьем законе Ньютона, можно утверждать, что на штангу со стороны груза действует сила Fr, горизонтальная и вертикальная составляющие которой показаны на рис. 8. Кроме этих сил на штатив действуют еще сила тяжести и сила реакции стола. По условию задачи масса штанги со стойкой достаточно мала, а основанием штатива является тонкий однородный диск. Следовательно, равнодействующая всех действующих на штатив сил тяжести Mg приложена к центру диска, как и показано на рисунке. При критической скорости вращения со стороны стола на штатив может действовать лишь сила, точка приложения которой совпадает с точкой О на краю диска, лежащей в вертикальной плоскости, в которой располагаются оси стойки и штанги штатива в данный момент времени (см. рис. 8). При этом положение штатива становится неустойчивым. Однако, как и при меньших угловых скоростях вращения, сумма всех действующих на штатив сил и сумма моментов этих сил относительно произвольной оси должны быть равны нулю, так как штатив все еще остается неподвижным. Отсюда следует, что алгебраическая сумма моментов силы тяжести Mg и силы Fr относительно горизонтальной оси, проходящей через точку О перпендикулярно указанной вертикальной плоскости, должна быть равна нулю, то есть
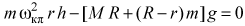 ,
,
поскольку плечо силы реакции стола относительно точки О равно нулю. Отметим, что из равенства нулю суммы всех действующих на штатив сил и моментов этих сил относительно указанной оси следует равенство нулю их моментов относительно любой параллельной ей оси. Так как линии действия всех приложенных к штативу сил лежат в указанной выше вертикальной плоскости, можно утверждать, что при выполнении последнего соотношения алгебраическая сумма моментов всех действующих на штатив сил относительно любой другой оси также будет равна нулю. Таким образом, искомая угловая скорость вращения груза, при которой основание штатива перестанет касаться всей плоскостью горизонтальной поверхности стола, равна
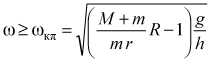 .
.
Читайте в любое время

