РЕШЕНИЕ ЗАДАЧ МЕХАНИКИ С ПОМОЩЬЮ ЗАКОНОВ СОХРАНЕНИЯ
Кандидат физико-математических наук В. ПОГОЖЕВ.
Публикуем последнюю часть задач по теме "Механика". Очередная статья будет посвящена колебаниям и волнам.
Задача 4 (1994 г.). С горки, плавно переходящей в горизонтальную плоскость, с высоты h соскальзывает небольшая гладкая шайба массой m. На плоскости стоит гладкая подвижная горка массой М и высотой Н > h. Сечения горок вертикальной плоскостью, проходящей через центры масс шайбы и подвижной горки, имеют вид, показанный на рисунке. На какую максимальную высоту х может подняться по неподвижной горке шайба после того, как она первый раз соскользнет с подвижной горки?
Решение. Горка, на которой первоначально находилась шайба, по условию задачи неподвижна и, следовательно, жестко скреплена с Землей. Если, как это обычно и делается при решении подобных задач, учитывать лишь силы взаимодействия шайбы с горками и силу тяжести, поставленную задачу можно решить, используя законы сохранения механической энергии и импульса. Лабораторную систему отсчета, как уже отмечалось в решении предыдущих задач (см. "Наука и жизнь" № 6, 2001 г.), можно считать инерциальной. Решение задачи разделим на три этапа. На первом этапе шайба начинает скользить с неподвижной горки, на втором - взаимодействует с подвижной горкой, а на последнем - поднимается вверх по неподвижной горке. Из условия задачи и сделанных предположений следует, что шайба и подвижная горка могут двигаться лишь поступательно так, чтобы их центры масс все время оставались в одной и той же вертикальной плоскости.
С учетом сказанного и того, что шайба гладкая, систему "Земля с неподвижной горкой - шайба" во время первого этапа следует считать изолированной и консервативной. Поэтому, согласно закону сохранения механической энергии, кинетическая энергия шайбы Wк=mv1 2/2 при ее движении по горизонтальной плоскости после соскальзывания с горки должна быть равна mgh, где g - величина ускорения свободного падения.
Во время второго этапа шайба вначале станет подниматься по подвижной горке, а затем, достигнув некоторой высоты, с нее соскальзывать. Это утверждение вытекает из того, что в результате взаимодействия шайбы с подвижной горкой последняя, как уже было сказано, к моменту окончания второго этапа должна двигаться поступательно с некоторой скоростью u, удаляясь от неподвижной горки, то есть в направлении скорости v1 шайбы в конце первого этапа. Поэтому даже если бы высота подвижной горки была равна h, шайба не смогла бы ее преодолеть. Учитывая, что сила реакции со стороны горизонтальной плоскости на подвижную горку, как и силы тяжести, действующие на эту горку и шайбу, направлены вертикально, на основании закона сохранения импульса можно утверждать, что проекция v2 скорости шайбы в конце второго этапа на направление скорости v1 шайбы в конце первого этапа должна удовлетворять уравнению
mυ1 = mυ2 + Mи (1)
С другой стороны, согласно закону сохранения механической энергии, указанные скорости связаны соотношением
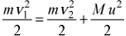 , (2)
, (2)
поскольку система "Земля - подвижная горка - шайба" оказывается при сделанных предположениях изолированной консервативной, а ее потенциальная энергия в начале и в конце второго этапа одинакова. Учитывая, что после взаимодействия с подвижной горкой скорость шайбы в общем случае должна измениться (v1 - v2 ≠ 0), и воспользовавшись формулой разности квадратов двух величин, из соотношений (1) и (2) получим
υ1 + υ2 = и (3)
а затем из (3) и (1) определим проекцию скорости шайбы в конце второго этапа на направление ее скорости перед началом взаимодействия с подвижной горкой
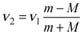 . (4)
. (4)
Из соотношения (4) видно, что v1 ≠ v 2 при m ≠ M и шайба будет двигаться к неподвижной горке после соскальзывания с подвижной только при m < M.
Применив вновь закон сохранения механической энергии для системы "Земля с неподвижной горкой - шайба", определим максимальную высоту подъема шайбы по неподвижной горке х =v22/2 g. После простейших алгебраических преобразований окончательный ответ можно представить в виде
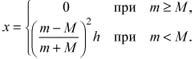
Задача 5 (1996 г.). Лежащий на горизонтальной плоскости гладкий брусок массой М прикреплен к вертикальной стене легкой пружиной жесткости k. При недеформированной пружине брусок торцом касается грани кубика, масса m которого много меньше М. Ось пружины горизонтальна и лежит в вертикальной плоскости, проходящей через центры масс кубика и бруска. Сдвигая брусок, пружину сжимают вдоль ее оси на величину ∆x, после чего брусок отпускают без начальной скорости. На какое расстояние передвинется кубик после идеально упругого удара, если коэффициент трения кубика о плоскость достаточно мал и равен μ?
Решение. Будем считать, что выполнены стандартные предположения: лабораторная система отсчета, относительно которой первоначально покоились все тела, инерциальна, а на рассматриваемые тела действуют только силы взаимодействия между ними и силы тяжести, и, кроме того, плоскость соприкосновения бруска и кубика перпендикулярна оси пружины. Тогда, учитывая заданное в условии положение оси пружины и центров масс бруска и кубика, можно полагать, что эти тела могут двигаться лишь поступательно.
После отпускания брусок начинает двигаться под действием сжатой пружины. В момент касания бруском кубика по условию задачи пружина должна стать недеформированной. Поскольку брусок гладкий и движется по горизонтальной плоскости, силы тяжести и реакции плоскости не совершают над ним работы. По условию массой пружины (а потому и кинетической энергией ее движущихся частей) можно пренебречь. Следовательно, кинетическая энергия поступательно движущегося бруска в момент касания им кубика должна стать равной потенциальной энергии пружины в момент отпускания бруска, а потому скорость бруска в этот момент должна быть равна 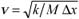 .
.
При касании бруском кубика происходит их соударение. При этом сила трения, действующая на кубик, изменяется от нуля до mmg, где g - величина ускорения свободного падения. Полагая, как обычно, что время соударения бруска и кубика мало, можно пренебречь импульсом силы трения, действующей на кубик со стороны плоскости, по сравнению с импульсом силы, действующей на кубик со стороны бруска за время удара. Поскольку смещение бруска за время удара мало, а в момент касания кубика пружина по условию задачи не деформирована, считаем, что пружина во время соударения на брусок не действует. Поэтому систему "брусок - кубик" во время соударения можно полагать замкнутой. Тогда, согласно закону сохранения импульса, должно выполняться соотношение
M v = MU + mu, (1)
где U и u - соответственно скорости бруска и кубика непосредственно после соударения. Работа сил тяжести и нормальной составляющей сил реакции плоскости, действующих на кубик и брусок, равна нулю (эти силы перпендикулярны их возможным перемещениям), удар бруска о кубик идеально упругий, и в силу малой длительности соударения смещением кубика и бруска (а следовательно, и работой сил трения и деформации пружины) можно пренебречь. Поэтому механическая энергия рассматриваемой системы должна оставаться неизменной и имеет место равенство
M υ2/2 = MU2/2 + mи2/2 (2)
Определив из (1) скорость бруска U и подставив ее в (2), получим 2Mvu=(M+m)u 2, а так как по условию задачи m << M, то 2vu=u2. Отсюда с учетом возможного направления движения следует, что кубик после соударения приобретает скорость, величина которой
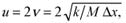 (3)
(3)
а скорость бруска останется неизменной и равной v. Следовательно, после удара скорость кубика должна превышать скорость бруска вдвое. Поэтому после удара на кубик в горизонтальном направлении вплоть до его остановки действует лишь сила трения скольжения μmg и, следовательно, кубик станет двигаться равнозамедленно с ускорением μg. На брусок же после соударения в горизонталь ном направлении действует только сила упругости пружины (брусок гладкий). Следовательно, скорость бруска изменяется по гармоническому закону, и, пока кубик движется, он опережает брусок. Из сказанного следует, что брусок от положения равновесия может сместиться на расстояние ∆х. Если коэффициент трения μ достаточно мал, повторного соударения бруска с кубиком не произойдет, а потому искомое смещение кубика должно быть
L = и2/ 2μg = 2k (∆x)2/ μM g.
Сопоставив это расстояние с ∆х, получим, что приведенный ответ верен при μ ≤ 2k ∆x/ M g
Задача 6 (2000 г.). На край доски, лежащей на гладкой горизонтальной плоскости, кладут небольшую шайбу, масса которой в k раз меньше массы доски. Шайбе щелчком сообщают скорость, направленную к центру доски. Если эта скорость больше u, то шайба соскальзывает с доски. С какой скоростью будет двигаться доска, если скорость шайбы будет в n раз больше u (n > 1)?
Решение. При решении задачи, как обычно, пренебрежем влиянием воздуха и будем считать, что система отсчета, связанная со столом, инерциальна, а шайба после удара движется поступательно. Отметим, что это возможно лишь в том случае, когда линия действия импульса внешней силы и центр масс шайбы лежат в одной вертикальной плоскости. Поскольку по условию задачи шайба при начальной скорости, меньшей u, не соскальзывает с доски, необходимо считать, что при скольжении шайбы по доске между ними действуют силы трения. Учитывая, что после щелчка шайба движется по доске к ее центру, а сила трения скольжения направлена антипараллельно относительно скорости, можно утверждать, что и доска должна начать двигаться по столу поступательно. Из ранее сказанного и закона сохранения импульса (поскольку доска находится на гладкой горизонтальной плоскости) следует, что скорость шайбы непосредственно после щелчка uш, ее скорость vш и скорость доски Vд в момент соскальзывания шайбы должны удовлетворять соотношению
muш = M Vд + mvш,(1)
где m - масса шайбы, а M - масса доски, если uш > u. Если же uш ≤ u, то по условию задачи шайба не соскальзывает с доски, и, следовательно, по прошествии достаточно большого промежутка времени скорости доски и шайбы должны стать равными. Полагая, как обычно, величину силы сухого трения скольжения не зависящей от скорости, пренебрегая размерами шайбы и учитывая, что перемещение шайбы относительно доски к моменту соскальзывания не зависит от ее начальной скорости, с учетом ранее сказанного и на основании закона изменения механической энергии можно утверждать, что при uш ≥ u
mu ш2/ 2 = MVд2/ 2 + mυш2/ 2 + A,(2)
где А - работа против сил трения, причем при uш > u Vд < v ш, а при uш=u Vд=vш. Учитывая, что по условию M/m=k, из (1) и (2) при uш=u после алгебраических преобразований получим
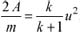 , (3)
, (3)
а так как при uш=nu из (1) следует, что
υш2 = n2и2 + k2Vд2 - 2nkи Vд (4)
искомая скорость доски должна удовлетворять уравнению
k (k + 1) Vд2 - 2nkиVд + kи2/(k + 1) = 0. (5)
Очевидно, что при n→∞ время взаимодействия шайбы с доской должно стремиться к нулю и, следовательно, искомая скорость доски по мере увеличения n (после того, как оно превысит некоторое критическое значение) должна уменьшаться (в пределе до нуля). Поэтому из двух возможных решений уравнения (5) условиям задачи удовлетворяет
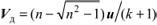 .
.
Читайте в любое время

