Яков Евсеевич Гегузин обладал незаурядным талантом физика и педагога — видеть простую суть сложного, восхищаться ею и уметь передать свою радость слушателю и читателю.

Книга Якова Евсеевича Гегузина «Капля» — для тех, кому интересны физика и природа. Для любопытных людей. В том числе и для тех, кто хочет работать или уже работает в науке.

Я. Е. Гегузин (1918—1987).

Наука и жизнь // Иллюстрации

Это большое счастье — зарабатывать на жизнь тем, что нравится делать. Наука даёт такое счастье любопытным и, конечно, способным радоваться узнаванию нового.

Но есть ещё и техника мышления в науке. Суть этой техники — стремление к ясности. Чёткое понимание тех простых законов, к которым, в конечном счёте, сводятся самые сложные с виду явления природы. Яков Евсеевич обладал незаурядным талантом физика и педагога — видеть простую суть сложного, восхищаться ею и уметь передать свою радость слушателю и читателю. О чём бы он ни рассказывал, он рассказывал интересно. Его книги такие же, какими были его увлекательные лекции. «Капля» — одна из лучших. А ещё есть «Пузыри», «Живой кристалл», «Почему и как исчезает пустота», «Очерки о диффузии в кристаллах».

Что общего между обычной каплей воды и атомным ядром? Как обнаружить, где пролетел электрон, позитрон или другая элементарная частица — меньше даже атомного ядра, с помощью обычного микроскопа? Как избирательное оседание капелек позволяет увидеть на зеркально гладкой грани кристалла рельеф из ступенек высотой 10 ангстрем, то есть одной миллионной доли миллиметра? Почему следы на поверхности пруда или лужи такие разнообразные? Как из порошинок получается монолитный прочный металл, то есть на чём основана порошковая металлургия? Почему и как растущий кристалл захватывает пузырьки газа или частицы, портящие его? Когда жидкость ведёт себя, как твёрдое тело?

Яков Евсеевич отвечает на все эти и многие другие вопросы, так или иначе связанные с физикой поверхности, с ясностью и строгой простотой физика, постоянно погружённого в мир этих явлений. И с живостью поэта. Он был поэтом и романтиком в науке, как и предмет его восхищения и любви — замечательный советский физик Яков Ильич Френкель (дефекты Френкеля, экситоны Френкеля, френкелевская теория деления атомного ядра, модель Френкеля — Конторовой движения дислокаций в кристаллах и т. д.). Яков Евсеевич любил, а потому и помнил стихи классиков и современников и любил читать эти стихи. Потому в «Капле» так много стихотворных цитат и эпиграфов. Он воспринимал природу и отношения между людьми ярко и неравнодушно, как поэт. Но, поражённый увиденным явлением, он анализировал его как физик, как настоящий профессионал. И эмоциональное восприятие физики вместе с неукротимой любознательностью поддерживало его в трудном и часто долгом пути к простому и изящному ответу.

XX век был веком физики, XXI называют веком биологии. Но, как говорят, «Господь Бог не берёт интегралов», то есть не заботится о том, как мы описываем и понимаем природу. Другими словами, природа едина. Тот уровень ясности и чёткого количественного понимания, которого достигла физика, ещё только маячит перед биологами и биохимиками из-за несопоставимо большей сложности их объектов. И конечно, этот уровень будет достигнут и для живых объектов. Компьютеры сделают это возможным, но только вместе с той идейной ясностью и простотой, которой учит настоящая наука, не делящаяся на «большую» и «малую», фундаментальную и прикладную. Книга Якова Евсеевича Гегузина проникнута духом такой единой науки о реальных явлениях. Кстати, поверхностные, или, как их ещё называют, капиллярные, явления в биологии работают ничуть не меньше, чем в физике и химии.

Книжка Я. Е. Гегузина учит думать и видеть единую природу как бы изнутри. Она даёт то видение мира, которое близко любознательным и глубоким людям.

Член-корреспондент РАН Александр Чернов.
(Из предисловия к книге.)

***

Шедевры научно-популярной литературы, созданные Я. Е. Гегузиным (1918—1987), стали доступны молодому поколению читателей. ИД «Интеллект» в 2014—2015 годах переиздал знаменитые «Каплю», «Пузыри», «Живой кристалл», «Очерки о диффузии в кристаллах».

Отрывок из книги: Гегузин Я. Е. Капля. — Долгопрудный: ИД «Интеллект», 2014.

Известно, что «капля камень долбит» — и в переносном, и в прямом смысле слова. В одном крымском селе я видел лежавшую у дома под крышей глыбу камня ракушечника, которая на полуметровую глубину была разрезана водяными каплями, падавшими во время дождя с крыши. Жестяная крыша оканчивалась ровной кромкой, и продолбленная каплями прорезь в камне эту кромку повторяла. В камне попрочнее каплям, возможно, не удалось бы сделать такую глубокую прорезь, а ракушечник, хрупкий и сыпучий, поддался, и вода разрезала его почти надвое.

Откуда у жидких, «мягких» капель эта способность долбить камень? Впрочем, быть может, это иллюзия, что вода во всех случаях жизни мягкая? Ведь если плашмя упасть на воду, можно убедиться, что она совсем не так уж мягка. А рука, медленно движущаяся в воде, свидетельствует об ином: вода легко расступается, уступая ей место. Одна и та же вода в одном опыте оказывается совсем не мягкой, а в другом — её мягкость вне сомнений.

Видимо, надо договориться о понятии слова «мягкий», вложить в него определённый физический смысл. Если мы каким-то движущимся предметом прилагаем усилие к некоторому телу и это тело послушно меняет свою форму, успевая следовать за движущимся предметом, мы говорим, что тело «мягкое». Уйдём от общих слов и будем рассуждать конкретнее. Пусть «движущийся предмет» — наша рука, а «некоторое тело» — вода. Если рука движется в воде медленно, вода мягкая, если же быстрым движением ударить рукой по воде, ощущается боль, несовместимая с представлением о мягкости. Всё дело в том, как успевает вода следовать за движением руки. Вода имеет вязкость, и поэтому скорость её реакции на движущуюся руку ограниченна, она не успевает следовать за «быстрой» рукой, препятствует её движению, и в этом случае ощущение мягкости воды исчезает: в момент удара по ней она ведёт себя подобно твёрдому телу.

Вернёмся к каплям, падающим с крыши на глыбу ракушечника, что лежит под ней.

Попробуем разобраться, что происходит с каплей, падающей на твёрдую поверхность. Вначале — о силе удара или, лучше, о давлении на поверхность, возникающем вследствие удара капли о неё. Чтобы это давление оценить, удобно представить себе не летящую каплю, а цилиндрическую струю, которая на своём пути встречает поверхность твёрдого тела. В оценке, которую мы получим, характеристики формы струи нет, поэтому она будет годна и для капли.

При внезапном столкновении струи с преградой последняя испытывает на себе действие так называемого гидродинамического удара. За этим научным термином стоит, в сущности, простое физическое явление: в момент столкновения струи с преградой в струе в направлении, противоположном её движению, начинает распространяться волна торможения. Наглядную иллюстрацию этому дал профессор Г. И. Покровский в книге «Гидродинамические механизмы». Он обратил внимание на внешнюю аналогию между заторможенной струёй и потоком автомашин, внезапно остановленным вспышкой красного света: у светофора возникает скопление машин, которое будет распространяться прочь от светофора, навстречу заторможенному потоку. Следует подчеркнуть, что сигнал о том, что поток автомобилей заторможен, движется со скоростью, меньшей скорости их движения, а волна торможения в струе движется со скоростью звука в воде, которая равна с = 1,5 · 10⁵ см/с и конечно же больше скорости капли, падающей с крыши.

Вспомним о том, что, согласно закону Ньютона, сила (F) есть произведение массы (m) на ускорение (а), которое, как известно, является отношением изменения скорости (∆ν) к времени (τ), в течение которого оно произошло. Этот закон можно записать в виде формулы

Fτ = m∆ν.

Масса струи, заторможенная за время τ, очевидно, равна

m = cτsρ,

где s — сечение струи; ρ — плотность жидкости. Так как изменение скорости остановленной струи равно скорости её движения, то закон Ньютона можно переписать в форме, определяющей давление Р = F/s, которое мы ищем:

P = ρνc.

Как и было обещано, полученная формула не содержит ни длины, ни сечения струи и ею можно пользоваться применительно к капле.

В полученной формуле ρ и с известны, а величину v следует обсудить. Интуиция подсказывает, что, когда скорость капли мала, близка к нулю, гидродинамического удара в полной мере не произойдёт. Капля расплющится, растечётся по поверхности, не ударив её.

Можно оценить наименьшую скорость, при которой произойдёт удар. Для этого, видимо, необходимо, чтобы за время удара капля не успела существенно расплющиться.

Чтобы капля в момент падения на камень вела себя подобно твёрдому шарику, необходимо, чтобы время её расплющивания (τ_р) было больше времени, в течение которого происходит удар (τ_у): τ_р > τ_у. Время τ_р близко к времени, в течение которого совершается одно колебание свободно летящей капли или воздушного пузырька, всплывающего в воде. С оценкой этого времени мы уже встречались: τ_р ~ Rη/α. А время τу можно оценить как отношение радиуса капли к скорости её полёта в момент падения на поверхность камня: τу ~ R/ν. Приблизительно за это время верхняя точка капли может долететь до камня, после того как нижняя точка его уже коснулась.

Теперь из условия τр ≈ τу легко оценить величину скорости падения капли, при которой она сможет «долбить камень». Эта скорость должна удовлетворять условию ν ≈ α/η.

При такой скорости давление, возникающее в момент удара, будет

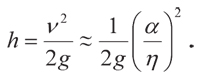
Так как ρ = 1 г/см³ · η = 0,1 г/(см · с), α = 70 дин/см, то Р ≈ 10⁸ дин/см² ≈ 10² кг/см². Многократно прикладываемое такое давление способно разрушить хрупкий ракушечник.

Пожалуй, интересней знать не скорость, с которой капля падает на камень-ракушечник, а высоту дома, у которого он лежит. Так как капля, оторвавшаяся от кромки крыши, падала свободно, высота дома и конечная скорость капли связаны простым и хорошо известным соотношением

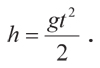
Очевидно, с учётом найденного выражения для ν интересующая нас высота дома должна удовлетворять условию

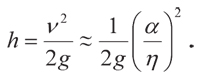
Сделаем численную оценку h. Вязкость воды η ≈ 0,1 г/(см · с), поверхностное натяжение α = 70 дин/см, g ≈ 10³ см/с², следовательно, высота дома должна быть около 2,5—3 м. Все эти вычисления, конечно, приближённые, и всё же результат получился разумный: одноэтажный сельский домик именно такую высоту обычно и имеет.

В приближённом расчёте мы предположим, что, оторвавшись от кромки крыши, капля долетает до ракушечника, не успев войти в «стационарный режим», когда её скорость перестаёт изменяться со временем. Надёжного права так считать у нас нет. Нас может извинить лишь получившаяся в расчёте разумная оценка высоты дома, достаточно низкого, чтобы «стационарный режим» не успел наступить. А мог бы расчёт оказаться и не благополучным, если бы ракушечник лежал не возле деревенского домика, а возле городского небоскрёба...

Последняя формула даёт возможность сделать любопытное предсказание. Если бы мы жили в мире глицериновых дождей, капли, падающие с меньшей высоты, чем водяные, приобретали бы способность долбить камень. Объясняется это большей вязкостью глицерина, а величина вязкости стоит в знаменателе формулы.

Информация о книгах Издательского дома «Интеллект» — на сайте www.id-intellect.ru

№9, 2016