Острейший и полный драматизма эпизод: Карабас-Барабас бегает за Буратино вокруг дерева, кончик бороды приклеивается к смолистому стволу, погоня продолжается…

Л. В. Владимирский. Иллюстрация к сказке А. Н. Толстого «Золотой ключик, или Приключения Буратино». 1955 год.

При наматывании борода постоянно расположена по касательной к стволу дерева. При этом Карабас (красная точка) описывает эвольвенту круга.

Схема сил в отклеиваемом элементе бороды.

Случай, когда отклеенный элемент бороды постоянно перпендикулярен стволу дерева. Длина жёлтого участка бороды равна длине красного.

Две кривые: эвольвента круга (красная) и архимедова спираль (синяя).

Снова две кривые вместе, но уже при очень длинной бороде.

Предлагаю рассмотреть всё вышеописанное с точки зрения не драматургии, а математики. Для этого нам, разумеется, придётся сделать ряд допущений. Прежде всего, сеньора директора театра будем считать материальной точкой, при всём глубочайшем уважении к его внушительным габаритам. В конце концов, нас интересует не всё его тело, а только борода и, скажем так, подбородок. Точнее, его траектория. Бороду же представим в виде тонкой нерастяжимой нити, ствол дерева «назначим» идеально круглым стержнем.

Собственно, ломать голову именно над этой задачей — значит изобретать велосипед. Ибо решена она задолго до рождения не только Карабаса-Барабаса в виде художественного образа из сказки «Золотой ключик, или Приключения Буратино», но и её автора Алексея Николаевича Толстого. Не будем топтать тропинку, уже протоптанную математиком Христианом Гюйгенсом. Скажем лишь, что «прикреплённый к подбородку» конец бороды описывает спиральную кривую, называемую эвольвентой круга. Знай об этом Карабас-Барабас, возможно, ему чуточку легче было бы пережить чувствительный контакт с деревом.

Прольётся ли ещё капля бальзама на душу директора кукольного театра, если ему рассказать о замечательных свойствах этой кривой и о том, например, что подавляющее большинство зубчатых колёс имеют именно эвольвентный профиль зубьев?

Для любителей формул приведём уравнение траектории в полярных координатах ρ и φ (с центром в центре дерева):

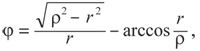
где r—радиус ствола.

Проявим гуманизм и дадим возможность Карабасу освободиться от дерева без помощи ножниц и иных режущих инструментов. В конце концов, борода — предмет особой гордости. Пусть же он отмотает её обратно!

Важный нюанс. Если приклеен только кончик бороды, то отмотает её Карабас без особых проблем и… без всякого интереса для нас с вами. Ибо эвольвентная траектория повторится «в обратной перемотке» и нам нечего будет рассматривать. Нет уж,простите, сеньор директор, пусть борода приклеится полностью, каждымсвоим сантиметром. Но не намертво, а так, чтобы её всё же можно было отклеить.

В чём разница? При наматывании (и свободном разматывании) борода постоянно расположена по касательной к дереву. Другое дело, когда борода приклеена. Оговорюсь, что глубоко погружаться в химические и физические свойства смолы не входит в нашу задачу. Никуда не денешься от некоторых условностей. Модель следующая: в каждой точке соприкосновения борода удерживается некой силой 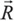, постоянной по всей окружности. И чтобы отклеить элемент бороды, необходимо усилие 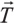, превосходящее радиальную составляющую этой силы .

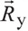Построим схему сил (рис. 1).

Углом α назовём угол между бородой и касательной к дереву. Из схемы понятно, что нулевым этот угол быть не может — тогда обнулилась бы и 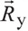, то есть отсутствовало бы усилие, отклеивающее бороду от дерева.

Теперь очевидно, что R^y = Tsinα. Именно эта реакция должна достичь необходимого для отклеивания элементарного участка бороды критического значения 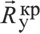, то есть

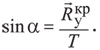
Учитывая, что входящие в правую часть равенства величины постоянны, неизменным будет сохраняться на протяжении всего разматывания и угол α. Каким именно будет этот угол, зависит от клейкости смолы и силы натяжения бороды.

Рассмотрим простейший случай, когда α = 90^о, то есть когда борода в каждый момент времени направлена вдоль радиуса.

В полярной системе координат легко заметить, что при повороте на произвольный угол Δφ (рис. 2) полярный радиус увеличивается на длину размотанного за это время участка бороды, то есть Δρ = OK'– OK = rΔφ.

А это условие определяет кривую, описываемую точкой K, как спираль Архимеда. Удивительно, но стоит намазать дерево смолой, и одна замечательная кривая обращается в другую, не менее замечательную!

Взглянем на обе кривые вместе (рис. 3а, б). На них зелёным цветом обозначен ствол дерева, красным — эвольвента круга, синим — архимедова спираль. Пунктир — начальный участок архимедовой спирали (рис. 3а), так как, если отвлечься от бороды и ствола дерева, эта кривая берёт старт с начала координат (в отличие от эвольвенты).

Легко заметить, что стоит Карабасу отдалиться от дерева, как две кривые становятся на удивление схожими, словно следуют параллельными курсами. Это впечатление ещё более усилится, если мы польстим длине бороды и рассмотрим несколько витков (риc. 3б).

А надо ли удивляться — борода-то одна и та же! Значит, и кривые просто обязаны быть близки одна к другой.

Если такое шуточное объяснение вас удовлетворит, отлично, если же нет, давайте повнимательнее приглядимся к уравнению эвольвенты круга.

Пусть Карабас уже далеко от дерева, то есть p ≫ r. Тогда

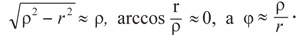
А это и есть уравнение архимедовой спирали!

Или, если выразиться строже:

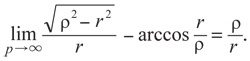
Простыми словами: чем дальше от центра, тем сложнее отличить эвольвенту круга от архимедовой спирали.

Конечно, эти «родственные связи» между двумя кривыми известны давно, но, пожалуй, никто, кроме нас с вами, не открывал их при помощи бороды!

№6, 2018