Эйнштейн и современная картина мира
Доктор физико-математических наук Б. БОЛОТОВСКИЙ.
Многие знают Альберта Эйнштейна только как автора теории относительности. Но его вклад в физику не исчерпывается одной теорией относительности. Были у него и другие работы, которые легли в основу современной науки.
Одна из этих трех замечательных работ называлась "О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты".
Во введении к статье Эйнштейн писал: "В этой работе будет показано, что согласно молекулярно-кинетической теории теплоты взвешенные в жидкости тела микроскопических размеров вследствие молекулярного теплового движения должны совершать движения такой величины, что [эти движения] легко могут быть обнаружены под микроскопом. Возможно, рассматриваемые движения тождественны с так называемым броуновским молекулярным движением; однако доступные мне данные относительно последнего настолько не точны, что я не мог составить об этом определенного мнения".
Молекулярно-кинетическая теория теперь считается твердо установленной, в ней никто не сомневается. Основные представления молекулярной теории преподаются в средней школе. Согласно этой теории все тела - газы, жидкости, твердые тела - состоят из атомов и молекул. Свойства тел определяются взаимодействием атомов и молекул, составляющих эти тела. Атомы и молекулы не находятся в покое, а совершают беспорядочное тепловое движение. В твердых телах атомы и молекулы колеблются вблизи положения равновесия, в газах и жидкостях могут перемещаться как угодно далеко. Кинетическая энергия, связанная с тепловым движением, пропорциональна температуре тела. Если T - температура тела, то среднее значение кинетической энергии молекул, составляющих это тело, пропорционально температуре:
,
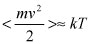Угловые скобки означают, что берется средняя величина кинетической энергии молекулы при температуре тела, равной T . Значок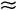 
означает "примерно равно" с точностью до множителя порядка единицы. Коэффициент - так называемая постоянная Больцмана:
,
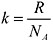где - универсальная газовая постоянная; а - число Авогадро (число молекул в грамм-молекуле). Существует точное выражение, связывающее среднюю кинетическую энергию теплового движения с температурой. Мы не будем его здесь выписывать, для нас достаточно приведенного приближенного соотношения.
Рассмотрим каплю жидкости при температуре T. Молекулы жидкости в этой капле находятся в непрерывном тепловом движении, причем среднее значение квадрата скорости <V2> можно определить из приведенной выше формулы, где - масса молекулы. Если же говорить не о квадрате скорости, а о самой скорости, то среднее значение скорости молекулы равно нулю - под ударами соседних молекул она с равной вероятностью может двигаться в любом направлении, и с каждым соударением направление это меняется.
Но как проследить за движением молекулы? Прямое наблюдение невозможно: молекула слишком мала, во много раз меньше длины волны видимого света. В оптический микроскоп ее не увидеть.
В 1905 году именно тот факт, что молекулы и атомы не поддаются прямому наблюдению, мешал полному признанию атомно-молекулярного строения вещества. В частности, крупнейшие физики того времени Эрнст Мах и Вильгельм Оствальд отвергали атомно-молекулярную гипотезу. Они считали, что можно говорить только о таких физических величинах, которые можно измерить, только о таких явлениях, которые поддаются прямому наблюдению. Если вводить какое-либо новое физическое понятие, необходимо дать способ его измерения или прямого наблюдения. А как можно увидеть атомы или молекулы? Видел ли их хоть один физик из тех, которые настаивают на их существовании?
В своей работе Альберт Эйнштейн рассмотрел поведение сравнительно крупной частицы, взвешенной в жидкости, например частицы цветочной пыльцы, помещенной в каплю воды. Такая частица приходит в состояние теплового равновесия с окружающей жидкостью. Средняя энергия теплового движения частицы, как и средняя энергия теплового движения молекулы, пропорциональна температуре:
.
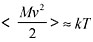Масса частицы намного больше, чем масса молекулы , поэтому средний квадрат скорости теплового движения у частицы гораздо меньше, чем у молекулы. Но все же частица пыльцы в капле воды не стоит на месте. Она перемещается под воздействием ударов со стороны окружающих молекул жидкости. Удары следуют со всех сторон, поэтому направление движения частицы меняется случайным образом, а средняя скорость перемещения равна нулю. Тем не менее, совершая случайные блуждания, частица медленно перемещается. Эйнштейн нашел закон этого перемещения. Он показал, что средний квадрат смещения частицы пропорционален времени движения. Напомним, что при равномерном движении не квадрат, а первая степень смещения пропорциональна времени движения (это просто путь, пройденный равномерно движущимся телом за данное время). Броуновское движение не является равномерным. Зависимость среднего квадрата смещения от времени, согласно Эйнштейну, имеет вид
.
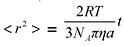Слева в этой формуле стоит средний квадрат смещения броуновской частицы за время . Справа - комбинация величин: - универсальная газовая постоянная; T - температура жидкости, в которой движутся броуновские частицы; Nа - число Авогадро; π=3,14… - число "пи", отношение длины окружности к ее диаметру; - вязкость жидкости, в которой находится броуновская частица; а - размер частицы. Чем больше вязкость жидкости, тем большее сопротивление она оказывает движению частицы. То же самое можно сказать и о размере частицы. Чем он больше, тем больше силы сопротивления, тормозящие движение частицы. Обычно размер броуновских частиц выбирался близким к одному микрону (см). Если размер выбрать меньше, частицу становится трудно наблюдать в микроскоп, а если размер превышает один микрон, броуновское движение частицы сильно замедляется.
Средний квадрат смещения пропорционален температуре жидкости Т (здесь T есть температура по шкале Кельвина, так называемая абсолютная температура). Чем выше температура, тем заметнее броуновское движение.
Читайте в любое время
