«Как можно не понимать, что такое логарифм, ведь это же так просто?» – порой совершенно искренне удивляются технари, наблюдая за математическими страданиями гуманитариев. А много ли среди вашего окружения людей, для которых математика подобна ночному кошмару, который, к счастью, закончился с выпускными экзаменами в школе? А может быть, вы сами из их числа?

Во многом причины ужаса и непонимания «царицы наук», как называл математику Карл Гаусс, уходят корнями в её преподаванием в школе, хотя, по правде сказать, это справедливо и для других предметов.

Довольно часто вместо того чтобы помочь понять и научить, школа навсегда отбивает всякий интерес к предмету, будь то математика или литература. Конечно, можно подходить к этой проблеме с позиции «естественного отбора», что если вы не смогли прочитать и понять учебник, то значит, эта дорога знания перед вами закрыта навсегда. Но есть ли другие решения, и можно ли дать учащимся более полное знание о мире, учитывая, а не игнорируя их индивидуальные способности?

В конце марта этого года в Москве прошла конференция «Психология и технологии математического образования», организованная компанией Яндекс и Международным обществом исследователей в области психологии математического образования. На конференции выступила Норма Пресмег – почётный профессор Иллинойского университета. В сферу её научных интересов входят такие темы, как визуализации в математическом образовании, решение и постановка математических задач, роль метафор и культуры в обучении математике и ее преподавании. «Наука и жизнь» публикует сокращённый вариант её доклада на прошедшей конференции.

Конференция «Психология и технологии математического образования» проходила 18–21 марта 2019 года в Москве. Фото: Yandex.

Почему различаются подходы к исследованиям математики и математического образования

– Математикам и исследователям математического образования не всегда удаётся найти общий язык: исследования математического образования не являются частью прикладной математики, между исследованиями в области чистой математики и исследованиями математического образования есть большие различия.

Математика – наука с тысячелетней историей. В сравнении с ней, исследования математического образования, которые существуют порядка ста лет – сущий «ребёнок». Развитие этой области исследований часто отсчитывают с 1908 года, когда в Риме был проведён первый Международный конгресс по преподаванию математики. Но на сегодня это уже сложившаяся научная отрасль, которая постоянно растёт, и важно принимать её самостоятельный статус.

Профессор Норма Пресмег. Фото: Yandex.

Теоретическая и эмпирическая эволюция в области исследования: количественные и качественные исследования

– В начале двадцатого века у исследователей математического образования в приоритете были строгие измерения, пришедшие из парадигмы естественных наук. С тех пор подход серьёзно изменился. Сейчас используются как статистические методы, так и качественные – но не менее точные, как мы убедились за эти десятилетия – методы: интервью и наблюдения.

Неизбежно возникает вопрос: как добиться в качественных экспериментах той же достоверности результата, строгой отчётности, которая есть в количественных методах, когда мы говорим о психологии, антропологии, философии – обо всём, что относится к внутреннему миру человека в процессе обучения.

Для этого мы, в частности, берём данные из разных (обычно трёх) источников: интервью, наблюдения в классе и отчеты школьников. Так же беседуем с одними и теми же интервьюируемыми несколько раз, возвращаясь к ним снова и снова за уточнениями.

Таким образом, качественные и количественные методы – это две стороны одной медали. Сейчас все большую популярность получает смешанная методология, где в рамках одного исследования используется сначала качественная методология, а потом количественная, или наоборот.

Что касается содержательных парадигм, то в первой половине двадцатого века преобладали бихевиористские теории. Исследования визуального мышления начались в конце 1970-х годов и основывались как на качественных, так и количественных методах. Качественные эксперименты имели даже большее значение, так как позволили получить представление о том, как работает визуальное восприятие в обучении математике, и в 1990-е годы визуализация получила признание как важная для исследований математического образования тема. Когнитивные и аффективные аспекты визуалиции – неотъемлемые компоненты систем репрезентации при решении математических задач.

Знал ли паук Cyrtophora moluccensis о гауссовой функции, когда плёл свою паутину? Фото:Frank Starmer/Flickr.com CC BY-SA 2.0

Исследования В.А. Крутецкого

– Многие докладчики на этой конференции так или иначе говорили о значении работ Л.С. Выготского и В.В. Давыдова, но я бы хотела назвать другое имя – Вадима Андреевич Крутецкого. Он сделал очень много для исследований математического образования, но его работы не были оценены по достоинству, и известны широкой публике меньше, чем работы его коллег. Препятствием более широкому и позитивному восприятию его работ стала как раз методология: в то время предпочтение по-прежнему отдавалось количественным методам, и его качественные наработки не вызывали должного доверия.

На протяжении тридцати лет Вадим Андреевич вёл исследования в области возрастной и педагогической психологии. Предметом его внимания были, в первую очередь, психология способностей и психология характера, он описал компоненты математических способностей. В 1969 году на английский перевели четыре его работы, в том числе «Психологию математических способностей школьников».

Крутецкий изучал детей всех возрастов, от малышей до подростков, пытаясь понять, что заставляет учеников одного и того же учителя по-разному подходить к решению одних и тех же математических задач. Он определял способность как индивидуальную черту, которая позволяет ребёнку выполнять задание быстро и правильно. Наследие Крутецкого важно в том числе потому, что он очень сильно опередил своё время.

Он выделил три типа учащихся:
– аналитический тип – учащиеся, у которых в первую очередь развито вербально-логическое мышление;
– геометрический тип – те, у кого развито наглядно-образное мышление;
– гармонический тип, для которого характерен баланс хорошо развитого словесно-логического и наглядно-образного компонентов.

Крутецкий попробовал выявить возрастные и индивидуальные особенности в соотношении вербально-логических и наглядно-образных компонентов мышления, а также особенности запоминания и воспроизведения. Я уверена, что мы до сих пор не смогли полностью оценить его разработки. Это настоящая сокровищница с задачами.

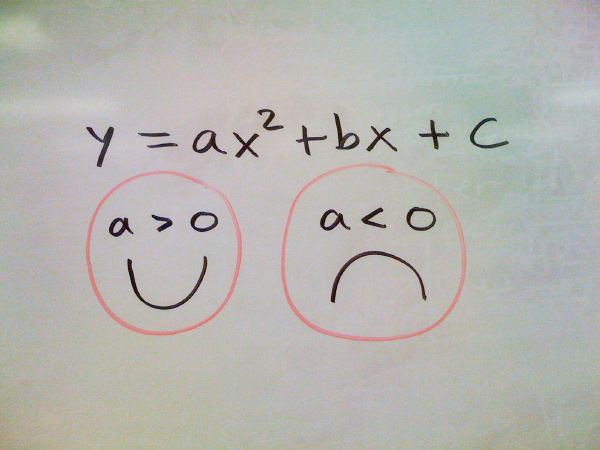
Чем отличается грустная парабола от весёлой параболы? Фото: Dan Bach/Flickr.com CC BY 2.0

Развитие идей Крутецкого в современных исследованиях

– Разница между теми учениками, которым математика даётся легче и теми, кому сложнее с ней разобраться, по результатам исследований В.А. Крутецкого, заключалась в умении увидеть формальную структуру задачи — «её скелет, освобождённый от всех конкретных значений и словно просвечивающий сквозь конкретные данные» (Крутецкий, «Основы педагогической психологии», 1972). То есть если ученики могли увидеть в задаче не отдельную, новую постановку проблемы, а соотнести её с имеющимися у них знаниями, решить её было легче. Влияние имеют и способности к логическому мышлению, обобщению, гибкость и ясность мышления.

Результаты его работы – и в частности, мысль, что визуальные образы могут помогать детям в решении математических задач с большей или меньшей степенью успешности, не в зависимости от наглядности материала, а в зависимости от того, насколько легко ученику удаётся увидеть на изображении математические отношения – во многом повлияли на изучение визуализации в математическом образовании, в том числе и на мою работу в последние тридцать лет.

Визуализация включает в себя как умственное представление изображений, так и внешние рисунки и схемы. Наиболее эффективным, по результатам моих исследований, оказался подход, когда педагоги использовали визуальные методы объяснения материала, но при этом обращали внимание на абстракцию и обобщения.

В целом, можно выделить пять типов зрительной образности:
– представление конкретных изображений,
– кинестетические представления (в том числе движение),
– динамические представления (изображение меняется),
– запоминание визуального образа формул,
– визуализация схем, связей между объектами без конкретных деталей.

Мозаика Пенроуза из дельтоидов. Фото: the pale side of insomnia/Flickr.com CC BY-NC-ND 2.0

Вопросы для будущих исследований

– Из моих исследований о роли визуальной составляющей в преподавании математики постепенно выросло целое направление, но перед исследователями математического образования по-прежнему множество вопросов. Сегодня много говорится об использовании технологий, и в этом контексте вопросы визуализации математических понятий становятся ещё более актуальными.

Какие аспекты педагогики важны для поддержки сильных сторон и облегчения трудностей использования визуального мышления в преподавании математики? Какие аспекты культуры общения в классе стимулируют активное использования визуального мышления в математике? Что делает изображения эффективными, когда они призваны помочь школьникам лучше понять математику?

Отдельно необходимо говорить и о роли метафор — как они должны использоваться в преподавании математики, чтобы помочь ученикам. И как вообще учитель может помочь ученикам связать между собой визуальные и символические изображения одних и тех же математических понятий. Параллельно возникает и следующий вопрос: как учителя могут использовать эмоции, возникающие при собственном образном мышлении, чтобы способствовать большему удовольствию от изучения и занятий математикой.

Все эти направления развиваются и изучаются не линейно. Сюда же вплелись семиотические исследования, понятие множественных репрезентаций, а сейчас активно развивается эмбодимент — понимание того, как телесные практики могут нам помочь. Таким образом, последние двадцать лет исследования визуального мышления начали включать в себя и изучение семиотических структур, и исследования жестов и движений педагога, и движений ребёнка.

Правильно ли собрали ленту Мёбиуса для детской площадки? Фото: Daniel Bowen/Flickr.com CC BY-NC-SA 2.0

Общество исследователей в области психологии математического образования

– Конференции Международного общества исследователей в области психологии математического образования (PME), где собираются учёные, увлечённые изучением математики через призму психологии, важны для всех, кто изучает математическое образование. Почти сорок лет – я езжу на эти конференции с 1980 – я своими глазами наблюдаю, как они влияют на то, что происходит в математическом образовании, какое невероятное значение они имеют. На первой конференции в Утрехте (Нидерланды) собралось 86 человек, а в 2014 году в Ванкувере (Канада) их было 865 – ровно в десять раз больше. Очень хочется видеть на этой конференции больше исследователей из России: пока, к сожалению, их можно пересчитать по пальцам одной руки.

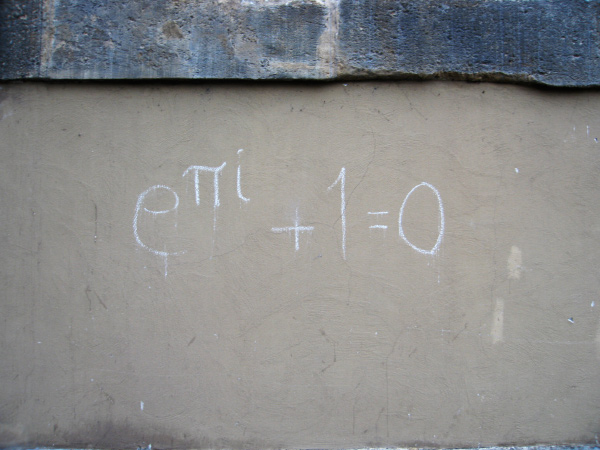
Тождество Эйлера. Иногда городское граффити бывает и таким. Фото: foam/Flickr.com CC BY-SA 2.0